Comment différencier les torchons des serviettes grâce au coefficient de Gini ?

Comment différencier les torchons des serviettes grâce au coefficient de Gini ?

Reconnaitre les torchons et les serviettes est un problème que nos aïeuls considéraient si important qu’ils en ont fait un proverbe. L’Intelligence Artificielle vient aujourd’hui à notre secours pour enfin résoudre ce dilemme.

La première question à poser lorsqu’on veut comprendre sur quels critères deux ensembles se distinguent, c’est :

« Quels sont les attributs à notre disposition pour décrire les systèmes étudiés ».

C’est la question la plus sensible. Par exemple, si vous cherchez à comprendre pourquoi les abricots que vous achetez en juillet sont plus sucrés que ceux que vous achetez en mai, et que chaque abricot est décrit par la couleur de l’étiquette ou la marque du tablier du vendeur, vous risquez de ne pas élucider votre question.

En data-mining, contrairement à beaucoup d’idées reçues, il vaut mieux avoir une intuition de la direction où chercher ou vous risquez de ne rien trouver.

Si on rajoute à l’exemple précédent les attributs : couleur du fruit, variété, nombre de jours d’ensoleillement et localisation du producteur, on peut espérer une réponse. Mais les attributs étant si nombreux, comment trouver celui qui a le plus d’impact ? En tant que client, si je n’avais le droit qu’à une question pour choisir le meilleur fruit, devrais-je la poser sur la durée d’ensoleillement ou sur la variété ?

Les méthodes à notre disposition dans le domaine de l’Intelligence Artificielle nous permettent d’apporter des réponses.

Les arbres de décision

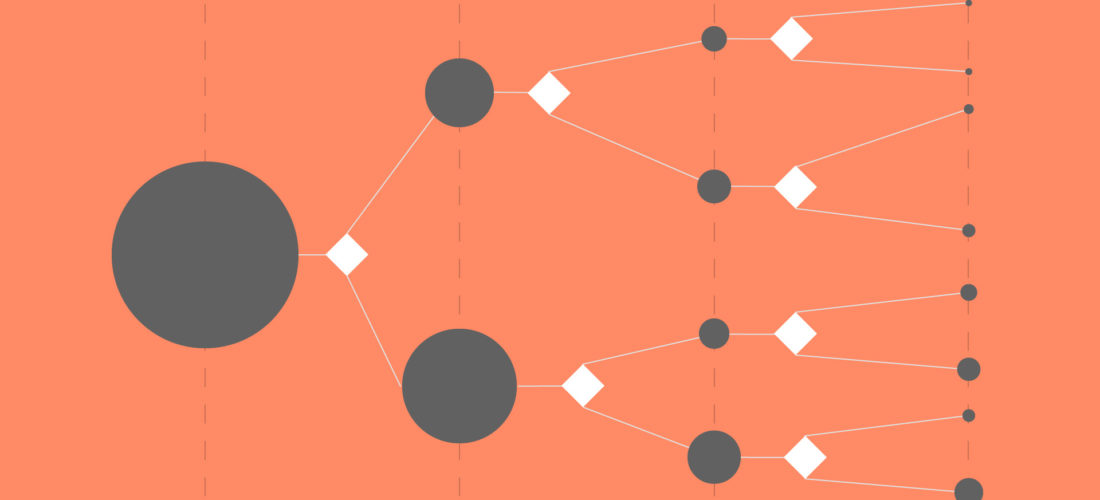
Les arbres de décision permettent de représenter graphiquement une succession de règles s’enchainant les unes aux autres. Ils ont pour objectif de réaliser une classification, souvent représenté par une séparation binaire.

Ce mode de représentation est utilisée dans les approches « Systèmes Experts », lorsque l’expertise métier peut être formalisée en une succession de règles. Mais ce n’est pas toujours le cas, et l’expérience a montré que la mise à jour de ces processus métier étaient difficile dans le temps.
Lorsqu’on n’arrive pas à dégager de règles, on utilise une approche basée sur l’analyse des données issues d’observations : le point de départ est un ensemble connu d’ « objets ». Chacun des objets est décrit par des attributs (par exemple couleur, provenance et variété). Chaque attribut admet plusieurs modalités (par exemple pour l’attribut couleur, les modalités peuvent être vert, jaune, orange). Enfin, chaque objet réussit ou non un test (par exemple, l’abricot est sucré ou non).

L’objectif est alors de déterminer, à partir de cet ensemble témoin, quelles sont les modalités d’attributs qui permettent d’obtenir des groupes suffisamment homogènes, pour qu’on puisse prédire le résultat du test, lorsqu’on s’intéresse à un nouvel objet. Par exemple, si un abricot est vert, quels que soient les autres attributs, on trouvera certainement qu’il appartient à la classe « non sucré ».

Il s’agit d’un apprentissage supervisé dans la mesure ou la méthode de sélection a été calibrée à partir d’échantillons dont on connait à l’avance le résultat du test.

Les arbres de décision sont très utilisés pour le data-mining ou l’aide à la décision :

• En fouille de donnée, ils permettent de mieux comprendre et caractériser les objets ou système qu’on manipule.
• Lorsque les règles de décision sont suffisamment tranchées, ils deviennent des outils d’aide au diagnostic.

Ils ont également un autre avantage, que ne possèdent pas les réseaux neuronaux pour le moment (de nombreux travaux sont en cours sur ce sujet) :

Les arbres de décision sont interprétables, c’est-à-dire qu’un utilisateur peut comprendre le cheminement qui a permis d’atteindre le résultat.

Pour les arbres de grande taille, le modèle global peut être difficile à appréhender, mais la classification sur un nœud est toujours compréhensible.

Le nœud de décision

La question est de trouver un algorithme qui permette, à partir d’un nœud racine, de séparer automatiquement une population d’objets, de manière itérative en créant des embranchements, jusqu’à obtenir les feuilles de l’arbre, c’est-à-dire des sous-groupes cohérents dans lesquels tous les objets répondent de la même façon au test. Tant qu’un nœud contient des objets qui répondent de façon différente au test, le processus d’embranchement continue.

Tous les objets d’un nœud intermédiaire ou d’une feuille sont décrits par une conjonction unique de conditions sur les attributs car les règles de décision sont mutuellement exclusives. Par exemple, si la décision de l’embranchement est réalisée sur la modalité « orange », tous les abricots de la 1ère branche seront orange et ceux de l’autre branche auront d’autre couleurs.

La fonction entropie et le coefficient de Gini sont des critères de différenciation fréquemment utilisés pour réaliser la séparation. Ces deux indices permettent de décrire l’homogénéité d’un groupe d’objets.

La fonction Entropie et le coefficient de Gini présentent leur minimum quand le groupe est totalement homogène.

Pour chaque nœud, l’objectif est de trouver l’attribut et ses modalités qui permettent d’obtenir la meilleure séparation du groupe, c’est-à-dire l’attribut et les modalités qui donnent le minimum pour l’indice de séparation choisi. Tant que le groupe d’objets contenus dans un nœud n’est pas homogène, chaque nœud voit apparaitre deux branches (arbres binaires) ou plusieurs branches (arbres n-aires). Les attributs considérés comme les marqueurs les plus différenciants sont donc proches de la racine de l’arbre.

Breiman et al. (1984) ont formalisé une méthodologie sous le nom de CART (Classification Algorithm and Regression Tree) qui génère des arbres binaires et utilise le critère de Gini comme critère de différenciation. C’est la méthode de classification la plus utilisée.

L’indice de Gini (lecture optionnelle)

L’indice de Gini est un outil mathématique qui mesure l’homogénéité d’une population. Il est par exemple utilisé par des organismes statistiques pour mesurer la répartition de la richesse dans un pays.
Dans le cadre de la méthode CART, on l’utilise pour mesurer l’homogénéité d’un ensemble d’objets pour un attribut donné, en regard d’un test binaire. Si on reprend nos abricots, on mesure l’indice de Gini pour chacun des attributs couleur, provenance et variété en fonction du résultat du test en deux classes «  sucré  / non sucré ». Si le test répond à plus de deux choix possibles (par exemple, « sucré/ moyennement sucré/ non sucré »), le test peut aussi se ramener à un test à deux choix : « appartient à la classe / appartient à une autre classe ».

1ère étape, calcul de l’indice de Gini
L’indice de Gini est basé sur la variance pour un ensemble d’objets répondant à un tests à deux valeurs possibles, caractéristique de la loi de Bernouilli. La variance mesure l’étendue d’un ensemble de données par rapport à un comportement moyen. Elle est définie comme la moyenne des carrés des écarts à la moyenne.
Dans le cas particulier de la loi de Bernouilli, si on désigne par p la proportion d’ objets en succès parmi l’ensemble des objets considérés, la variance est égale à

Considérons un attribut et ses m modalités. Pour l’ensemble de Nm objets ayant cette modalité, dont le test comprend j choix ou classes possibles, l’indice de Gini est la somme des variances pour chaque classe :

On va utiliser cette formule pour mesurer l’homogénéité de chaque ensemble d’objets définis par un couple attribut/modalité.

Si l’attribut couleur possède trois modalités vert, orange et jaune, on calculera 3 indices.

Plus l’indice est faible, plus l’ensemble est homogène. Il est donc probable que l’indice du couple « couleur/verte » soit faible, voire nul si on prend l’hypothèse que tous les abricots verts sont non sucrés. Mais il est aussi probable qu’il y ait peu d’abricots verts en vente. Il faut donc pondérer l’indice de la modalité par la proportion d’individus pour valider que la couleur soit un critère prioritaire de sélection.
C’est l’objet de la seconde étape du calcul.

2ième étape : Priorisation des attributs
Pour chaque attribut (par exemple couleur), si N est le nombre total d’objets, Nm le nombre d’individu pour la modalité m de l’attribut (par exemple vert) et im l’indice de Gini pour cette même modalité, l’indice de Gini pour l’attribut s’écrit :

On choisit l’attribut avec l’indice le plus faible, puis la modalité au sein de l’attribut qui a également l’indice le plus faible. Le nœud se sépare en deux sous-groupes : les objets décrits par cette modalité et les autres. Puis on recommence l’opération sur les deux sous-groupes avec les couples attributs/modalités restants.

Est-ce que ca marche ?

Ca dépend.
La qualité des attributs est la clé de la réussite. En partant du principe que l’échantillon d’objets est suffisant pour que le système puisse « apprendre » correctement, il reste quelques écueils :

• Si la séparation ne dépend pas des attributs considérés, on ne trouvera rien de cohérent (par exemple Attribut = « Marque du tablier du vendeur »)
• Si une conjonction de conditions sur les attributs (par exemple Couleur = Orange ET Provenance = Roussilon ET Variété = Jumbocot) contient des objets répondant différemment au test, on obtiendra une marge d’erreur plus ou moins acceptable, qui correspond à l’hétérogénéité des feuilles.
• Si la situation évolue régulièrement (par exemple, pour les abricots, en fonction des mois de l’année), il faudra prévoir une réactualisation du modèle avec la même périodicité. Un upgrade logiciel peut remettre en cause un modèle de diagnostic établi pour de la maintenance prédictive.

Cependant, dans tous les cas, les arbres de décision ont un puissant avantage par rapport à d’autres méthodes comme les réseaux neuronaux : ils permettent à l’utilisateur d’accéder au modèle. L’utilisateur visualise rapidement si l’analyse des données a du sens et pourquoi elle en a (ou pourquoi elle n’en a pas).

Pour illustrer ce point, reprenons l’exemple de l’attribut « Marque du tablier du vendeur ». Il se peut que tous les abricots sucrés soient vendus par des vendeurs habillés avec le même tablier tandis que les autres vendeurs achètent des tabliers de marques différentes. Cet attribut devient le marqueur le plus important, et apparait en premier lieu dans l’arbre de décision. A l’utilisateur de décider si il est pertinent de le laisser ou de l’enlever de la liste des attributs. Un attribut étrange qui ressort comme fortement discriminant dans un arbre doit toujours être interprété avant d’être rejeté. L’utilisateur profite de cet avantage pour perfectionner l’arbre et l’aide à la décision.

Les approches « système expert » et « par analyse d’observations » sont complémentaires. Elles s’enrichissent l’une l’autre pour aboutir au meilleur des deux mondes.

Dans la pratique

Dans la pratique, on considèrera le plus souvent des arbres avec peu d’étages, dits peu profonds. Un arbre profond sera plus difficile à appréhender et probablement dépendant du jeu de test utilisé pour réaliser l’apprentissage. Le cas extrême est celui d’un modèle qui ne trouve sa pertinence que lorsqu’il y a autant de feuilles que d’objets. Cela veut dire que le modèle n’a pas trouvé de couple attribut/modalité qui permette de faire des groupes homogènes de plusieurs individus. Il est certain que rajouter de nouveaux objets dans le jeu d’apprentissage fera évoluer le modèle. Il s’agit d’un problème classique en apprentissage, nommé le sur-apprentissage : il faut que le modèle soit suffisamment robuste pour que si le jeu de test change, le modèle reste identique.

Si on arrête volontairement l’arbre après quelques étages, il est possible que les feuilles contiennent des objets qui ne soient pas totalement homogènes, c’est-à-dire qu’elles contiennent des objets de plusieurs classes. Mais l’objectif n’est pas forcément d’avoir une décision fiable à 100% mais d’accompagner la décision avec une marge d’erreur acceptable.

Si un sous-groupe contient un nombre important d’objets et que les objets répondent à 95% favorablement au test, on peut estimer que les attributs le caractérisant sont une bonne approximation d’un test réussi. Par exemple, en maintenance prédictive, il ne serait pas économiquement rentable de déplacer un technicien pour changer une carte si la probabilité de défaillance future est de 50%. Par contre, si elle avoisine les 85%, cela devient intéressant.

On cherche donc à construire un arbre qui soit le plus réduit possible avec la plus petite marge d’erreur. Il faudra souvent réaliser un compromis entre performance et stabilité. A performance comparable, on préférera toujours le modèle le plus simple.

Maintenant que vous êtes familiers avec le modèle le plus connu de classification, il ne reste plus qu’à l’appliquer à la reconnaissance des torchons et des serviettes. La première question est :

« Quels sont les attributs à notre disposition pour décrire les objets étudiés » ?

Pas facile… Bienvenue dans le quotidien du data scientist.

Références :

Breiman, Leo; Friedman, J. H.; Olshen, R. A.; Stone, C. J. (1984). Classification and regression trees. Monterey, CA: Wadsworth & Brooks/Cole Advanced Books & Software. ISBN 978-0-412-04841-8